When Spheres Collide
If I can't use my own blog to post nicely worked out math problems, then what good is it?
So the other day, I had a problem to solve. I had two circles (the initial problem was in 2D, but the solution works for spheres in any number of dimensions). The circles were moving in what I can assume are straight lines, and I want to know when (if ever) they will intersect.
Start with some definitions. I'll specify the circles with initial position and velocity (vectors, as you can tell from the little arrows over them) and radius. Then each one's position (position of the center) can be expressed in a simple vector equation as a function of time:

Now here's where it gets clever. I make a change of frame (a trick I learned from many Physics problems). I'll consider it from the point of view of circle 1. From that point of view, circle 1 is sitting at the origin, not moving, while the position and velocity of circle 2 can be expressed as a new moving circle which (for lack of imagination) I will call circle 3. While I'm at it, I'll give circle 3 a radius equal to the sum of that of circles 1 and 2:
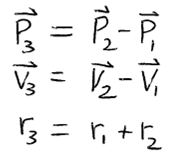
Now the problem is reduced to a SINGLE moving circle and we want to know when (if ever) it will touch the origin. Express distance (of the edge of the circle) from the origin and start solving. Double vertical bars is length (of a vector) and other places use the dot product of vectors.

Okay, I've simplified that some. Now let's solve for when it touches. That would be when d(t) = 0.
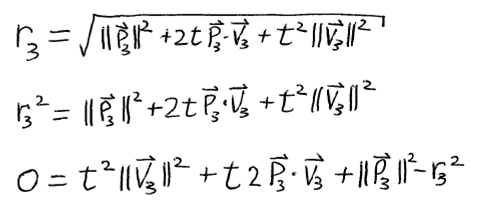
It's actually not very messy, but we can make it incredibly neat by defining a few terms:

Giving us this form:

Oh, I think I recognize that one. In fact, I have the solution memorized:

Q.E.D.
[Okay, so this was a problem solved, not a proof so I shouldn't write "Q.E.D.". But like I said: it's my blog, if I can't have fun, what good is it?]